O que é Word2Vec

Word2Vec é um método de Aprendizado de Máquina para construir um modelo de linguagem baseado em ideias de Aprendizado Profundo. No entanto, a rede neural usada tem apenas uma camada escondida.

Resumindo: Word2Vec é como o “Hello, world!” do Plano de Linguagem Neural (PLN). Porém, é preciso um pouco mais de trabalho além de escrever algumas linhas de código.

Pequenos esclarecimentos antes de começarmos

Para os propósitos deste artigo, não é tão importante que você entenda os detalhes das diferenças entre Inteligência Artificial, Aprendizado de Máquina (Machine Learning) e Aprendizado Profundo (Deep Learning). No entanto, estes termos muitas vezes são confundidos e usados como sinônimos, o que quase sempre está errado. Para esclarecer:

1. O Aprendizado Profundo (Deep Learning) lida com um tipo específico de Rede Neural (redes neurais profundas, com muitas camadas, ou redes rasas que contêm muitos dados de entrada e nós interdependentes).
2. O Deep Learning é uma área de estudo inserida na área de Aprendizado de Máquina (Machine Learning).
3. O Machine Learning, por sua vez, faz parte da área de Inteligência Artificial.

---

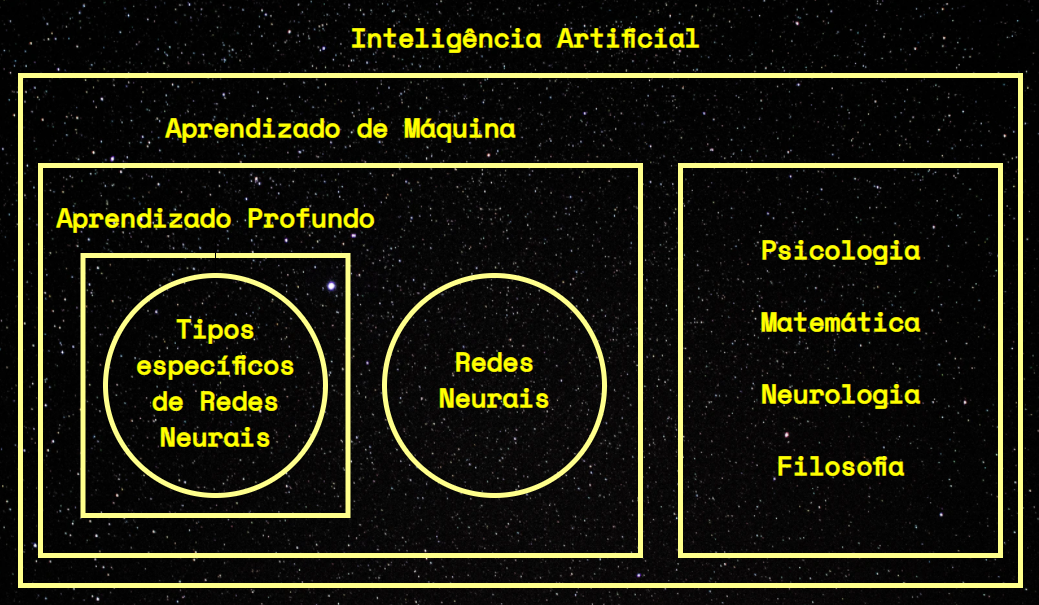
Neste artigo, vamos construir um modelo de linguagem baseado em ideias de Aprendizado Profundo, usando métodos de Aprendizado de Máquina.

Veja também como a edrone usa a Inteligência Artificial na Recomendação de Produtos Personalizados em suas ferramentas de Automação de Marketing para E-commerce!

---

Como surgiu o Word2Vec?

A invenção do Word2Vec (e seus clones: Doc2Vec, Nodes2Vec) aconteceu entre 2013 e 2015. A onda mais recente começou em 2017 com a invenção do BERT (e também GPT, T5).

O que é Word2Vec?

Word2Vec é uma técnica de Processamento de Linguagem Natural (PLN) baseada em uma tese popularizada por John Rupert Firth no fim da década de 1950. Esta tese diz que cada palavra é caracterizada, e até certo ponto definida, pelas outras palavras em seu entorno.

Firth, por sua vez, baseou sua teoria na ideia de Zellig Sabbettai Harris, publicada em 1954, de que “palavras que ocorrem em contextos semelhantes tendem a ter significados semelhantes”.

Se pensarmos bem, é uma ideia surpreendentemente certeira. A Hipótese Distribucional é a base para a Semântica Estatística e, embora tenham se originado na Linguística, estes assuntos têm atraído muita atenção nas áreas de ciências cognitivas e Aprendizado de Máquinas.

Posicionamento das palavras no corpus de textos: a base da Semântica Computacional

Juntando tudo: quanto mais uma palavra “A” aparecer no mesmo contexto que outras palavras específicas (por exemplo, “B”, “C”, “D” e “E”), mais próximo será o significado de todas estas palavras. O contexto, neste caso, depende do critério de quem estiver fazendo a análise. Pode ser a mesma frase, o mesmo parágrafo, ou – mais provável quanto o assunto é PLN — o mesmo trecho que usamos para analisar o corpus do texto.

Você poderia presumir que, quanto maior o texto, mais precisas serão as previsões, o que está corretíssimo. O tamanho do trecho, no entanto, é uma escolha do analista. Aqui, maior nem sempre é melhor.

Como funciona o Word2Vec?

Então, por onde devemos começar ao analisarmos um texto? Primeiro, precisamos fazer o texto ser compreensível para computadores. O nome Word2Vec (“Word to Vector“) já indica — precisamos transformar palavras em vetores.

OK, e o que são vetores? Um vetor, em programação, serve para armazenar variáveis de um mesmo tipo. Para facilitar a compreensão, entenda “vetor” como uma sequência unidimensional de elementos. No caso do Word2Vec, atribuímos uma lista de valores numéricos a cada palavra original presente no texto.

Tutorial Word2Vec

É sempre mais fácil explicar usando exemplos, então vamos acompanhar o passo a passo usando um pequeno corpus apresentado a seguir. Mas antes, um pequeno aviso a respeito da linguagem de programação que usaremos para este exercício.

Usaremos a linguagem de programação Python para lidar com os conceitos de Aprendizado de Máquina. Se você domina esta linguagem, sugerimos continuar a leitura com um ambiente preparado e seu editor de texto favorito à mão.

Se você nunca usou Python, não se preocupe. A instalação é gratuita e fácil. Eu usei o Spyder como ambiente de desenvolvimento integrado. Após instalar estas ferramentas, basta copiar e colar os códigos apresentados e testar os processos por conta própria.

Além disso, não tem problema se o código for incompreensível para você. Não é necessário entender como o código funciona para entender como o Word2Vec funciona. Foque apenas no resultado 🙂

Vamos criar um corpus!

Para este exemplo, nosso corpus terá apenas duas frases:

edrone is awesome. The first CRM for eCommerce and AI fueled marketing machine.

Código:

tiny_corpus = ['edrone is awesome', 
               'The first CRM for eCommerce and AI fueled marketing machine']
print(tiny_corpus,'n')

Resultado:

['edrone is awesome', 
 'The first CRM for eCommerce and AI fueled marketing machine'] 

---

O uso de letras maiúsculas e minúsculas faz diferença, então precisamos deixar tudo em minúsculas (apresentado abaixo para mostrar os estágios de tokenização):

Código:

# LOWER CASE
tiny_corpus_lowered = [sentence.lower() for sentence in tiny_corpus]
print(tiny_corpus_lowered,'n')

Resultado:

['edrone is awesome', 
 'the first crm for ecommerce and ai fueled marketing machine'] 

---

Agora vamos dividir as frases em palavras separadas.

Código:

# TOKENIZATION
tiny_corpus_lowered_tokenized = [sentence.split() for sentence in tiny_corpus_lowered]
print(tiny_corpus_lowered_tokenized,'n')

Resultado:

[['edrone', 'is', 'awesome'], 
['the', 'first', 'crm', 'for', 'ecommerce', 'and', 'ai', 'fueled', 'marketing', 'machine']]

---

A esta altura, o pré-processamento está quase pronto. Agora vamos construir um dicionário para o nosso pequeno corpus.

Como você pode ter percebido, a lista de palavras foi inicialmente dividida em uma lista bidimensional (matriz). Para criar o dicionário, vamos primeiro organizá-la em uma lista de palavras originais em ordem alfabética, e depois transformá-la em uma lista unidimensional.

Código:

# DICTIONARY
words = [word for sentence in tiny_corpus_lowered_tokenized for word in sentence]
print(sorted(words),'n') 

unique_words = list(set(words))

Resultado:

['ai', 'and', 'awesome', 'crm', 'ecommerce', 'edrone', 
 'first', 'for', 'fueled', 'is', 'machine', 'marketing', 'the'] 

---

Agora vamos criar o dicionário, concluindo o processo de pré-processamento!

Código:

# ASSIGN TO DICTIONARY
id2word = {nr: word for nr, word in enumerate(unique_words)}
print(id2word,'n')

word2id = {word: id for id, word in id2word.items()}
print(word2id,'n')

Resultado:

{0: 'is', 1: 'ai', 2: 'first', 3: 'ecommerce', 4: 'the', 
 5: 'fueled', 6: 'machine', 7: 'for', 8: 'awesome', 
 9: 'and', 10: 'marketing', 11: 'crm', 12: 'edrone'} 

{'is': 0, 'ai': 1, 'first': 2, 'ecommerce': 3, 'the': 4, 
 'fueled': 5, 'machine': 6, 'for': 7, 'awesome': 8, 
 'and': 9, 'marketing': 10, 'crm': 11, 'edrone': 12} 

Codificação Distribuída (One-Hot Encoding)

O processo de transformar palavras em vetores está quase concluído. Agora vamos atribuir um vetor a cada palavra da lista. Confira o código abaixo, e mais adiante discutiremos o resultado.

Código:

# ONE HOT ENCODING
from pprint import pprint
import numpy as np

num_word = len(unique_words)
word2one_hot = dict()

for i in range(num_word):
  zero_vec = np.zeros(num_word)
  zero_vec[i] = 1
  word2one_hot[id2word[i]] = list(zero_vec)
  
# RESULT
pprint(word2one_hot)

Resultado:

{'ai': 
 [0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],

 'and': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0],
 
 'awesome': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0],
 
 'crm': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0],
 
 'ecommerce': 
 [0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
 
 'edrone': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0],
 
 'first': 
 [0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
 
 'for': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0],
 
 'fueled': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
 
 'is': 
 [1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
 
 'machine': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
 
 'marketing': 
 [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0],
 
 'the': 
 [0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0]}

E pronto!

Simplificando o Word2Vec

Como você pode ver, cada palavra única tem seu próprio vetor. Estes vetores não são como os que você aprendeu nas aulas de física – eles não fazem sentido fisicamente, pois estão em um espaço de 13 dimensões, tornando-os impossíveis de serem imaginados. Felizmente, não precisamos fazer isso!

Para simplificar:

1. Cada palavra original em nosso texto representa uma dimensão.
2. Cada vetor é representado por zeros (“0.0”) e apenas um “1.0”.
3. Cada “1.0” aparece em uma posição diferente.

Ou seja, se nosso texto fosse composto por 100 palavras originais, cada vetor seria composto por 99 “0.0” e apenas um “1.0”, e cada “1.0” estaria em uma posição diferente para cada palavra. Esta convenção permite que os computadores processem palavras facilmente.

E como os vetores são processados? É aí que entra o Modelo SkipGram.

O que é SkipGram?

O Skip-Gramé um modelo que indica o contexto de um documento a partir de uma palavra específica que foi selecionada. Para isso, ele usa as relações semânticas entre as palavras.

Colocando o Modelo Skip-Gram em prática

Quanto mais vezes duas palavras aparecerem no mesmo contexto, mais próximos serão seus significados. Para fazer esta análise, usamos uma definição precisa, um contexto de determinado tamanho.

O tamanho do trecho depende do critério do analista, então vamos usar um tamanho de dois – isso significa que vamos analisar cada palavra no corpus em relação às duas palavras que aparecerem imediatamente antes e depois dela, conforme o esquema abaixo:

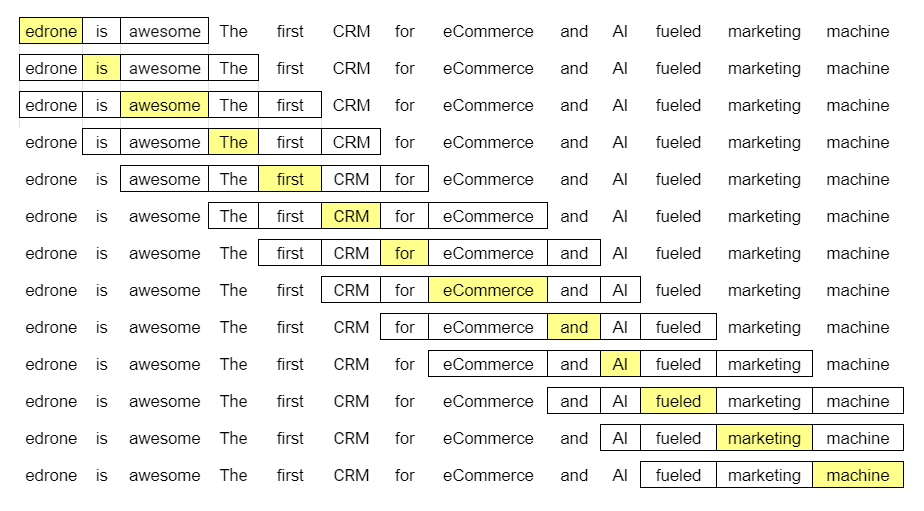
Na primeira linha temos:

• (edrone, is)
• (edrone, awesome)

Na segunda, temos:

• (is, edrone)
• (is, awesome)
• (is, the)

Na terceira:

• (awesome, edrone)
• (awesome, is)
• (awesome, the)
• (awesome, first)

Estes pares, traduzidos em linguagem de máquina, ficam assim:

(edrone, is) ->

-> ([0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0],

[1.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0])

…e assim por diante.

Usando o modelo Skip-Gram, a tarefa da nossa rede neural será aprender a relação entre uma palavra específica, usada como dado de entrada, e a palavra que está em seu entorno, que será fornecida como dado de saída.

Camada de entrada, camada oculta e camada de saída

Se você já teve algum contato com Aprendizado de Máquinas (Machine Learning) ou Aprendizado Profundo (Deep Learning), talvez reconheça o gráfico abaixo.

Vamos deixar o nosso corpus e vetores originais de lado por enquanto. Para explicar melhor os mecanismos por trás de uma Rede Neural, vamos usar como exemplo um corpus menor, de apenas seis palavras originais. Assim será mais fácil compreender como o processo funciona.

Como temos seis palavras originais, isso significa que seus vetores, cada um composto por uma sequência numérica única de cinco “0.0” e um “1.0”, serão embutidos (word embedding) em seis dimensões. No lado esquerdo do gráfico temos a camada de entrada (input layer), no meio a camada oculta (hidden layer) e à direita, a camada de saída (output layer). Neste exemplo, decidimos usar três nódulos, ou neurônios, na camada oculta. Assim como o tamanho do contexto, o número de nódulos também é uma escolha do analista.

Quando treinamos esta rede com os pares de palavras, a entrada (input) é um vetor one-hot representando a palavra de entrada, e o dado de saída de treinamento (training output), que nós determinamos, também é um vetor one-hot representando a palavra de saída.

O dado de saída (output) de fato – não o de treinamento – será gerado pela rede neural após ela ser treinada. Agora, o dado de entrada continuará sendo um vetor one-hot representando uma palavra, mas o dado de saída será uma distribuição de probabilidade formada por diferentes valores de ponto flutuante (ou seja, não serão vetores one-hot). Mas voltaremos ao dado de saída mais tarde.

A primeira metade do gráfico pode ser representada pela seguinte equação:

[  begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 end{bmatrix} times begin{bmatrix} 1 & 2 & 2\ -1 & 0 & -2\ 1.2 & 1 & -1\ -0.5 & -1 & 2\ -1 & 0 & -1\ 1 & 2 & -1 end{bmatrix} =begin{bmatrix} 1.2 & 1 & -1 end{bmatrix} ]

A matriz representa as conexões entre os nodos, com diferentes pesos atribuídos a elas. Aqui, estes pesos foram determinados aleatoriamente a título de exemplo, mas à medida que a rede neural aprende (veremos como isso acontece mais adiante), esta matriz é automaticamente atualizada.

Se você é bom em álgebra linear, talvez esteja pensando: “Espera um pouco… se o vetor é composto majoritariamente por zeros, eu consigo facilmente calcular esta matriz de cabeça.” Qual é a pegadinha?

Quando você multiplica um vetor one-hot por uma matriz, está efetivamente selecionando apenas a linha da matriz que corresponde ao “1.0” no vetor. Em nosso exemplo, seria a terceira linha da matriz, que tem os valores (1.2, 1 e -1).

Ou seja, estamos usando o “1.0” do vetor one-hot como um indicador, e a camada oculta age como uma tabela de consulta (lookup table).

Porém, nós temos vetores de seis dimensões em ambos os lados. A segunda parte da equação é semelhante, e faremos um novo cálculo usando outra matriz.

Desta vez, o dado de saída (output) não está mais tão claro – e o mais importante, não aponta a uma direção específica, pois não é um vetor one-hot.

Para extrair um resultado útil deste dado de saída, usaremos a função de ativação softmax:

[ {frac{e^{x}}{sum e^{x}}} ]​

Ao aplicar a função softmax, nosso resultado será:

Note que a soma dos valores é igual a 1!

O resultado é uma lista de probabilidades para os vetores correspondentes no dicionário (lista de palavras com as quais começamos). Em outras palavras, cada linha representa a probabilidade daquela posição conter o número “1.0” no vetor one-hot  de saída. No exemplo abaixo, o resultado indica que a palavra de saída (output) com a maior probabilidade de estar certa é a representada pelo vetor [1.0, 0.0, 0.0, 0.0, 0.0, 0.0] em nosso dicionário.

A diferença entre o vetor de saída, baseado em probabilidade, e o vetor alvo (a palavra “correta”) é crucial para que a rede neural possa aprender.

Modelo Skip-Gram e CBOW: Duas abordagens ao Word2Vec

Este é um bom momento para mencionarmos que existem duas abordagens principais ao Word2Vec: o Modelo Skip-Gram e o Continuous Bag of Words (CBOW). Em poucas palavras:

• Modelo Skip-Gram: indica o contexto (palavras ao redor) a partir de uma palavra específica que foi selecionada como input.
• CBOW: prevê uma palavra central, com base nas palavras ao redor que foram usadas como input.

Como você pode perceber, uma abordagem é o inverso da outra. Neste exemplo, usamos o modelo Skip-Gram: tomamos uma palavra específica, e observamos as previsões de palavras de entorno fornecidas pela rede neural.

Qual técnica é melhor? Isso vai depender do seu objetivo. Independentemente de qual você usar, a arquitetura das redes neurais será mais ou menos parecida. A diferença é qual informação nós usaremos como dado de entrada.

E como aplicar este resultado? Como ensinar à rede se ela está acertando ou errando?

Faremos isso aplicando a Função de Perda (Loss Function).

Função de Perda: Entropia cruzada

Assim como o vetor de entrada,  o vetor-alvo é one-hot: composto por vários “0.0” e um único “1.0”. O vetor softmax, por outro lado, é composto por tudo menos “0.0” e “1.0”. Compará-los é crucial para entender se a nossa rede neural está fazendo um bom trabalho ou falhando. Para isso, usaremos a entropia cruzada, uma das muitas funções de perda possíveis.

Fórmula de entropia cruzada:

[ {H(p,q)=-sum _{x} p(x) log q(x)} ]

Para usá-la, pegamos nosso vetor-alvo e nosso vetor softmax:

[ overrightarrow{V_T} = [1.0, 0.0, 0.0, 0.0, 0.0, 0.0] newline overrightarrow{V_S} = [0.411, 0.411, 0.151, 0.001, 0.000, 0.024] ]

Inserimos os vetores na fórmula:

[ H(overrightarrow{V_T},overrightarrow{V_S}) = – [  overrightarrow{V_T} cdot ln ( overrightarrow{V_S} ) ]  ]

[ H = – [  0 cdot ln ( 0.411 ) + 1 cdot ln ( 0.411 ) + … + 0 cdot ln ( 0.024 ) ] ]

Note que, novamente, o vetor one-hot age como um indicador!

[ H = – [  1 cdot ln ( 0.411 ) ] = 0.478]

A entropia cruzada indica a distância entre a previsão da nossa rede neural e a resposta desejada (vetor-alvo). O que podemos fazer com esta informação?

Propagação Retrógrada: Gradiente Descendente Estocástico

Para máquinas, “aprender” significa minimizar o valor do erro.

Nossa função é encontrar o mínimo da função de perda. Redes neurais atualizam os pesos das relações entre os nódulos para minimizar o valor da entropia cruzada. Isto não pode ser visualizado facilmente pois, como você sabe, estamos lidando com um espaço multidimensional.

Porém, para explicar como funciona, vamos simplificar e apresentar um exemplo em espaço 3D: são duas dimensões para os pesos (os valores abstratos que iremos ajustar) e a terceira dimensão indica o valor da entropia cruzada.

Cada combinação de pesos resultará em um valor diferente, e o processo de otimização envolverá “descer a ladeira” até chegar ao valor mais baixo possível. Quanto mais baixo for este valor, mais próximo estaremos da previsão correta!

Em suma, estamos comparando quão longe nossa previsão está do resultado desejado, e atualizando os nódulos para que a rede obtenha melhores resultados. Esta é uma representação simplificada de como o algoritmo funciona, mas infelizmente o Word2Vec é um pouco mais complicado.

Conclusão sobre o Word2Vec

O exemplo apresentado é a versão mais simples possível do (já relativamente simples) Word2Vec, que foca na previsão de palavras.

Enquanto isso, também queremos treinar o modelo, mais ou menos “matando dois coelhos com uma cajadada”. Porém, o modelo de aprendizagem que apresentamos é pouco eficiente devido às seguintes razões:

• Uma “rodada” é chamada de época. Ela cobre o período em que nossa rede neural está processando todos os exemplos de treinamento. No “mundo real”, não se usa apenas seis palavras, mas sim milhões delas.
• Geralmente, o treinamento de uma rede neural envolve mais do que uma época. Muito mais.
• À medida que o vocabulário cresce, também cresce o número de dimensões. Vetores de seis dimensões são muito mais fáceis de se processar do que vetores com milhões de dimensões.
• Nós estamos calculando a probabilidade de ocorrências de palavras ao mesmo tempo em que estamos usando estes resultados para atualizar a rede neural. Não é necessariamente ruim, mas funciona melhor como um método de otimização do que de aprendizado.

Em outras palavras

O método apresentado envolve gerar um resultado e então dizer à máquina se ela tomou uma decisão certa ou errada. Na prática, estamos torcendo por previsões corretas para depois “empurrá-las” através da rede neural.

É como dar um problema de matemática para uma criança pela primeira vez, observá-la enquanto ela se debate para resolver, e no fim dizer “errado, a resposta certa é 5”. E fazer isso de novo e de novo. Não é muito didático, concorda?

Em vez disso, podemos mostrar exemplos de respostas certas e erradas sem perder tempo com os cálculos, pois sabemos que a criança (no caso, a rede neural) ainda não foi treinada. Chamamos isso de Skip-Gram com Amostragem Negativada.

Skip-Gram com Amostragem Negativa

A ideia aqui é apresentar à máquina um par de palavras, e já dizer se elas aparecem no mesmo trecho ou não!

Se as palavras estiverem no mesmo trecho, daremos um valor de “1”. Se não, o valor será “0”. Nesta abordagem, teremos duas palavras (a palavra analisada e a palavra-alvo) como dado de entrada, e o dado de saída será o valor correto (“1” ou “0”). E como ficam os exemplos incorretos?

As respostas de treinamento que são erradas (verdadeiro negativo) são geradas usando a palavra analisada e uma outra palavra retirada aleatoriamente do texto e que não está no trecho da palavra analisada.

Você se lembra do corpus que analisamos anteriormente?

Usando este corpus como exemplo e aplicando o modelo Skip-Gram com Amostragem Negativa (Skip-Gram with Negative Sampling – SGNS), as primeiras amostras poderiam ser algo como a imagem abaixo. Para fins didáticos, eu escolhi duas amostras negativas para cada amostra positiva. Assim como o tamanho do trecho, o número de amostras negativas é uma escolha do analista!

Skip-Gram com Amostragem Negativa na Prática

Agora vamos usar duas matrizes:

• Matriz de valores embutidos – representa as palavras de entrada (input)
• Matriz de contexto – representa as palavras-alvo

Como sempre, no início estaremos trabalhando com valores aleatórios. Mas não se preocupe, logo faremos os ajustes!

Vamos agora observar o processo de treinamento. Como ele funciona?

1. Escolhemos um vetor da matriz de valores embutidos e um da matriz de contexto.
2. Calculamos o produto deste par de vetores.
3. Aplicamos uma função logística ao resultado, de forma que o resultado seja um valor entre 0 e 1.
4. Subtraímos o valor da relação “pertence ou não pertence ao trecho” (1 ou 0).
5. Como resultado, teremos a margem de erro referente a cada vetor (tanto o de entrada como o da palavra-alvo), permitindo que nossa rede neural seja ajustada.

O processo acima é aplicado em cada par de palavras de treinamento, e então repetido de novo (e de novo) por todo o vocabulário até atingir a precisão desejada. Após terminarmos nosso processo de pré-treinamento, vamos guardar a matriz de valores embutidos para uso posterior.

Esse foi apenas um resumo do Word2Vec pelo Modelo SkipGram para uma análise superficial e inicial dessas funcionalidades – que vão muito além dos exemplos mostrados aqui!

Quer saber mais sobre Machine Learning e Inteligência Artificial? Veja nosso conteúdo sobre a Lei de Benford.